The Cave & The Quadrivium: Mathematics in Classical Education

by Dr. Jeffrey S. Lehman

University of Dallas

What place should the study of mathematics have in classical education? Most classical schools rightly emphasize the linguistic arts of the trivium—grammar, logic, and rhetoric—but few have thought through (much less implemented) the mathematical arts of the quadrivium—arithmetic, geometry, music, and astronomy—in a meaningful way. This is not to say, of course, that classical schools do not study mathematics; rather, it is simply to point out that the classical liberal arts of mathematics have little, if any, influence on the way mathematics is considered and taught in most classical schools. Are these quadrivial arts, in contrast to those of the trivium, simply outmoded today? If so, why? If not, how might they inspire and be incorporated into the curricula of classical schools? In order to answer these questions, we must first begin by getting a clear sense of what the quadrivial arts are, as well as what they are not. To do so, we will turn to Plato’s Republic, one of the fountainheads of education in the Western tradition.

Book VII of Republic contains two of the most remarkable passages in all of Plato’s dialogues. The first, the image of the cave (514A-521B), compares the effect of education (and its lack) on the human soul to the experience of being shackled in a subterranean prison. The second passage, the mathematical plan of studies described immediately after the cave image (521C-531E), is presented by Socrates as the remedy for man’s imprisoned condition, the means by which he is able to be liberated and to ascend to the full light of the sun. Ironically, while the image of the cave is arguably the most remembered passage in Plato’s works, the mathematical means of ascent—the proposed solution to our predicament—often goes unnoticed. In what follows, let us take a look at these two passages, focusing principally on the way Plato (through Socrates) presents a vision of these mathematical studies as distinct yet related means of ascent from lower to higher things.

Meditations on the Cave Image

Part of the delight of the cave image is its inexhaustibility. The more we reflect upon the image together with what precedes and follows it, the more we find to wonder about. Thus, in these comments on the cave we will not attempt to plumb the depths of this image in any comprehensive way (if that were even possible); instead, our purpose is to focus attention on those aspects of the cave image that best prepare us to receive the mathematical plan of studies that follows in Book VII. With this purpose in mind, let’s see what we can find.

As was mentioned above, Socrates presents the image of the cave as a likeness to “the effect of education and of the lack of it on our nature” (514A). Socrates calls on Glaucon (and us, the readers of the dialogue) to exercise our imagination:

Imagine human beings living in an underground, cavelike dwelling, with an entrance a long way up, which is both open to the light and as wide as the cave itself. They’ve been there since childhood, fixed in the same place, with their necks and legs fettered, able to see only in front of them, because their bonds prevent them from turning their heads around. Light is provided by a fire burning far above and behind them. Also behind them, but on higher ground, there is a path stretching between them and the fire. Imagine that along this path a low wall has been built, like the screen in front of puppeteers above which they show puppets (514A/B; emphasis added).¹ Plato, Republic, trans. G. M. A. Grube, rev. C. D. C. Reeve (Indianapolis: Hackett Publishing Co, 1992). All quotations of Plato’s Republic are from this edition.

After Socrates describes people along this low wall who use statues of men and animals to cast shadows on the wall in front of the prisoners, Glaucon comments, “It’s a strange image you’re describing, and strange prisoners” (515A). Socrates replies: “They’re like us” (ibid.).

I have conveyed the kernel of this passage for two reasons. First, notice the significant place of images and the imagination in the tale. Rather than draw everything out for Glaucon, Socrates exhorts him repeatedly to imagine—to take an active part in creating this image of the soul in its lack of education in his mind’s eye. This active engagement of the imagination is crucial to the ascent that follows. Second, as strange as it sounds to Glaucon (and to us!), this image is meant to bear a true likeness to our own benighted condition without education. What exactly is so disturbing about the image? Of course, no one would wish to be physically bound; but the prisoner’s predicament is far worse than simply a loss of freedom of movement. The chains are themselves an image of an even more coercive force, one that leaves the prisoners in the dark about what really is. As Socrates points out, the prisoners “would in every way believe that the truth is nothing other than the shadows of those artifacts” (515C). Another way of putting it is to say that they mistake images for the more substantial realities of which they are images. Because the prisoners cannot “turn around” to see the machinations of the puppeteers, they take the shadows to be things themselves and thus are unaware of the true cause of what they see.

After giving us a clear image of the soul in a state of ignorance, Socrates describes what happens when a prisoner is freed and ascends out of the cave. “I suppose,” Socrates remarks, “that he’d need time to get adjusted before he could see things in the world above. At first, he’d see shadows most easily, then the images of men and other things in water, then the things themselves. Of these, he’d be able to study the things in the sky and the sky itself more easily at night, looking at the light of the stars and the moon, than during the day, looking at the sun and the light of the sun” (516A/B). Having been habituated to see only the images right in front of him, it takes time and effort for the former prisoner to embrace his newfound freedom. Furthermore, his ascent to knowledge has a certain order to it: first, he comes to sees shadows for what they really are—namely, shadows and not the things of which they are shadows; then, he apprehends the reflections of men and other creatures in water, able in time to discern the difference between these reflections and that of which they are reflections. In each case, perceiving the “lower” thing—a shadow, a reflection—become a means of truly coming to know a “higher” thing. Fundamental to this ascent is the ability to perceive an image as an image. As Socrates puts it, the one who ascends from the cave of ignorance into the light of knowledge is able to “know each image for what it is and also that of which it is the image” (520C). Contrary to a common caricature of Plato’s thought, he is not a “dualist” who exalts the intelligible realm at the expense of the sensible realm. Moreover, he does not seek to do away with images, as if one could use the images as a ladder to reach higher things and then kick the ladder away once the ascent is accomplished. Rather, perceiving images as images is vital to the process of coming to know; both the movement from image to the thing itself and the movement back again from thing to image are necessary for teaching and learning.

The one who perceives an image as an image recognizes at least three things: 1) the image, 2) that of which it is an image, and 3) the necessary relation between the two. Thus, when we come to realize that an image is an image of something, we attain some awareness—however partial, perspectival, and incomplete—of what lies beyond the image. This insight regarding images sheds light on comments Socrates makes about “causes” in this passage. For instance, in the quotation from 516A/B above, Socrates says that the one making his ascent will proceed from a study of “the things in the sky and the sky itself … at night, looking at the light of the stars and the moon” to “looking at the sun and the light of the sun” during the day. Significantly, the ascent described here ends with the sun, presented elsewhere in Republic as an image of the good (506D ff.). What is more, “at this point [the aspirant to knowledge] would infer and conclude that the sun provides the seasons and the years, governs everything in the visible world, and is in some way the cause of all the things that he used to see” (516B/C; emphasis added). Note well that the one who successfully ascends to the contemplation of the sun is then able to look back at what has come before and see that “in some way” these lower things are caused by the sun. A moment’s reflection reveals that what is true of the sun on a grand scale is also true of lesser things. In other words, just as the sun is the cause of lower things in the visible world, so also is every “thing itself” the cause in some sense of its own image. To give a simple example, the tree (together with the sun, of course) is the cause of the tree’s shadow. The ascent to higher things is paired with a subsequent descent back to lower things, rendering them more intelligible in the process.

Before turning to a treatment of the mathematical plan of studies that follows the image of the cave in Book VII, a few general comments about images and the imagination are in order. We live in a culture saturated with images. Through cell phones, the Internet, television, printed images and other media, the average person is presented with myriad images every day, far more images, one could argue, than at any previous time in human history. Given this unprecedented inundation with images, one might expect that the imagination would flourish. Instead, for most of us these images simply overpower our imaginative power, leaving us glutted with images and yet starved for the kind of nourishment that would make our imagination strong and healthy. Like the people chained in Plato’s cave, our imaginations are enthralled by appearances; and those with enthralled imaginations are much easier to manipulate and control. One key factor leading to the impotence of imagination today is the absence of any serious discipline or formation of the imagination. To be a passive recipient of empty and deceptive images is one thing; to be an active former of true and beautiful images is another. This is where the quadrivial arts come in. Let us return to Book VII of Plato’s Republic to begin to see how these mathematical arts can form the imagination, making possible the ascent to higher studies.

Imagination, Mathematics, and Ascent

Once the interlocutors have completed their account of the cave and discussed its implications for the education of rulers in their ideal city, Socrates poses the following question: “Do you want us to consider now how such people will come to be in our city and how—just as some are said to have gone up from Hades to the gods—we’ll lead them up to the light?” (521B/C). After Glaucon’s hearty affirmative response, Socrates continues: “This isn’t, it seems, a matter of tossing a coin, but of turning a soul from a day that is a kind of night to the true day—the ascent to what is, which we say is true philosophy” (ibid.). This reference to “turning the soul” underscores a distinction made earlier in the account of the cave, namely, the difference between a “stamping” and a “turning” education. First mentioned in Book II, the stamping education is described by Socrates as suitable for the young: “You know … that the beginning of any process is most important, especially for anything young and tender? It’s at that time that it is most malleable and takes on any pattern one wishes to impress upon it” (377A/B). As a signet ring may be impressed upon molten wax, leaving the form of the ring embedded in the receptive material, so the education of the young is compared to impressing the malleable minds of students with an external teaching, placing it “in” their minds from without. The stamping image of education is not challenged in Book II. Here in Book VII, however, Socrates gives the impression that a stamping education attempts the impossible: “Education isn’t what some people declare it to be, namely, putting knowledge into souls that lack it, like putting sight into blind eyes” (518B/C). Given this critique of stamping education in Book VII, one might wonder whether there is any place for such education in the broader scheme of teaching and learning. Addressing this question is clearly beyond the scope of this essay; for now, suffice it to say that the turning education commended in Book VII is clearly presented as superior to the stamping education of Book II. And more to the point, Socrates identifies such turning education with the ascent made possible through the mathematical plan of studies he is about to describe. After briefly reminding us of the basic training in gymnastic (for the well-ordered body) and music (for the body and the soul) advocated earlier in Book II (376E ff.), Socrates then proceeds to outline the mathematical studies that will make the ascent possible.

The first mathematical study mentioned is number and calculation, “that inconsequential matter of distinguishing the one, the two, and the three” (522C). Socrates remarks that arithmetic is a “common thing that every craft, every type of thought, and every science uses and that is among the first compulsory subjects for everyone” (ibid.). While common and compulsory in some form, Socrates is at pains to point out that arithmetic as it is customarily studied and used is not conducive to the ascent and freedom he envisions. He contends that “no one uses it correctly, … as something that is really fitted in every way to draw one towards being” (523A). Socrates makes a distinction among sense perceptions: some “summon” the understanding to look into them, others do not. “The ones that don’t summon the understanding are all those that don’t go off into opposite perceptions at the same time. But the ones that do go off in that way I call summoners—whenever sense perception doesn’t declare one thing any more than its opposite, no matter whether the object striking the senses is near at hand or far away” (523B/C; emphasis in original). For an example, Socrates asks Glaucon to consider his fingers—“the smallest, the second, and the middle”—and then Socrates explains:

It’s apparent that each of them is equally a finger, and it makes no difference in this regard whether the finger is seen to be in the middle or at either end, whether it is dark or pale, thick or thin, or anything else of that sort, for in all cases, an ordinary soul isn’t compelled to ask the understanding what a finger is, since sight doesn’t suggest to it that a finger is at the same time the opposite of a finger (523C/D).

Once Glaucon agrees, Socrates turns to the various opposites that are present in our perception of these same three fingers—bigness and smallness, thickness and thinness, hardness and softness, etc. Anyone who attentively considers the matter realizes that perceiving a finger as one finger among many involves something more than mere sensation. In other words, to count fingers requires some ability—however imperfect—to judge what counts as a finger. Without some inchoate knowledge of the nature of things, a knowledge that passes beyond the opposite sense perceptions we typically receive when perceiving multiple instances of the same kind of thing, we are unable engage in “that inconsequential matter of distinguishing the one, the two, and the three.” In order to do so, our imagination must be able to submit its objects to reason so that they can be judged by reason. Socrates explains:

Reason it out from what was said before. If the one is adequately seen itself by itself or is so perceived by any of the other senses, then, as we were saying in the case of fingers, it wouldn’t draw the soul towards being. But if something opposite to it is always seen at the same time [e.g., bigness and smallness, thickness and thinness, hardness and softness, etc.], so that nothing is apparently any more one than the opposite of one, then something would be needed to judge the matter. The soul would then be puzzled, would look for an answer, would stir up the understanding, and would ask what the one itself is (525D/E).

On the one hand, it is obvious that the imagination receives something from the senses in order to form images. The ability that the imagination has of faithfully capturing what it receives from the senses is absolutely essential to the possibility of retaining any awareness of what we have sensed in the past. On the other hand, the imagination is not—or at least it should not be—the slave of the senses. Instead, the images of our imagination are themselves considered and judged by our understanding. This twofold ability of imagination—to receive from the senses and to serve the understanding—makes possible the “turning away” from the merely sensible and toward what is truly intelligible.

In order to see this a bit more clearly, let’s consider the second mathematical art presented by Socrates, namely, geometry. As was the case with arithmetic, in his account of geometry Socrates is keen to distinguish what he is talking about from what those who practice geometry typically say about it. Speaking of these practitioners, Socrates claims, “They give ridiculous accounts of it, though they can’t help it, for they speak like practical men, and all their accounts refer to doing things. They talk of ‘squaring,’ ‘applying,’ ‘adding,’ and the like, whereas the entire subject is pursued for the sake of knowledge” (527A/B). Notice the difference between the two geometers in terms of purpose: the one who practices geometry for the sake of measuring parcels of land, determining heights or perimeters of buildings, etc., always engages in geometry for practical ends—that is to say, his knowledge is for the sake of something else; the one who pursues the kind of geometry Socrates has in mind seeks knowledge for its own sake. This difference in end also implies a difference in the role of imagination. For the practical geometer, the imagination need never pass beyond the senses. After all, the objects created by practical geometry, once produced, will occupy the same sensible world where his measurements began. Thus, there is no need for the practical geometer to trouble himself with considering the nature of geometrical objects in themselves. The practical geometer as practical geometer is not (and should not be) bothered by the fact that, try as he may, he cannot draw a line that is absolutely straight, or create a circle whose radii are exactly equal. Doing so would take him beyond the practical, workaday concerns of land measurement, building construction, and the like.

The geometer of Socrates has fundamentally different ends and therefore employs different means. It is precisely the geometrical objects themselves that concern him. Thus, he wants to know what a point is, what a line is, what a circle is, and so on. Furthermore, when he does his “constructions” he wants to be able to form geometrical figures and solids not in the sand or on a whiteboard, but in his imagination. The constraints of the sensible realm that limit the practical geometer do not limit him. Although the liberal art of geometry clearly owes its origins to practical geometry, by abstracting from the sensible realm and its conditions the liberal art of geometry can effectively turn away from a total immersion in the sensible realm in order to see what can be known about geometrical objects in themselves and for their own sake.

Perhaps an example would be helpful here. Let’s consider the first proposition in Euclid’s Elements, the greatest introduction to geometry ever written. In this proposition, Euclid sets out to construct an equilateral triangle on a given straight line (AB). In order to do so, he first uses the straight line AB to describe two circles. He then draws straight lines from one of the points of intersection (C) to create the lines CA and CB, as in the diagram below:

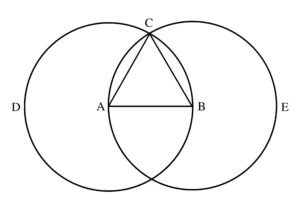
Given that all the radii of a given circle are equal to one another, Euclid proves that AC and AB must be equal to one another; for the same reason, BA and BC also must be equal. Since two things (AC, BC) are each equal to the same third thing (AB, which, of course, is the same as BA), those same two things (AC, BC) must be equal to one another. Thus, all three lines (AB, BC, CA) are equal and we know that Euclid has constructed an equilateral triangle, ABC.

This simple proposition clearly illustrates the difference between the two types of geometers and their respective geometries. If the geometer of Socrates (and Euclid) were using an actual straightedge and compass to construct his lines and circles, he obviously could never prove this proposition. For the purposes of practical geometry, on the other hand, a line that is for the most part straight and a circle whose radii are approximately equal is sufficient. If greater accuracy is needed, the practical geometer can try to avail himself of tools and procedures that would fit the bill. But for the one who engages in the liberal art of geometry, any deviation from strict equality among the radii will make the proof absolutely break down, since the argument only follows if the radii are in fact equal. Thankfully, he is not strictly speaking constructing the figure in his diagram, but rather in his imagination. So while our geometer uses diagrams to illustrate what he is attempting to prove, such diagrams are never meant to instantiate the truths in question. Rather, the diagrams serve simply as mediators between minds—the one teaching the proof, the other(s) learning it.

Quadrivial Studies and the Foothills of Philosophy

At this point, let’s stop and take a retrospective glance at the ground we’ve covered. This essay began with a few general questions about the nature and status of the quadrivial arts. In order to make headway on these questions, we examined two passages from Book VII of Plato’s Republic. Our examination of the cave image drew attention to the importance of images and the imagination in making an ascent from the cave of ignorance into the light of knowledge. Recognizing an image as an image was vital to the movement upwards. And the imagination, while clearly tied to and reliant upon sensation, also served higher purposes. In our brief consideration of two of the quadrivial arts, arithmetic and geometry, we caught a glimpse of how these mathematical studies could help to bring about a turning away from unreflective immersion in sensation and a turning toward higher things. Central to this turning was the way in which the imagination could aid the understanding, being used by the understanding to help it render judgments about things that transcend sensation and point toward intelligible things. Finally, in considering geometry we saw the imagination at work, not merely receiving images but actually constructing geometrical objects under the direction of the understanding. These objects, though inspired by our encounter with the sensible realm and in some sense rooted in that realm, nevertheless transcend that realm and direct us toward still higher things.

Earlier in the essay, we noted that Socrates identified a training in these mathematical studies with “the ascent to what is, which we say is true philosophy.” A remarkable claim, to be sure. Even more remarkable, though, is what Socrates says of them a little further on. While discussing the quadrivial plan of studies, Glaucon makes a passing comment about the “usefulness” of the study of astronomy: “a better awareness of the seasons, months, and years is no less appropriate for a general than for a farmer or navigator” (527D). Socrates replies:

You amuse me: You’re like someone who’s afraid that the majority will think he is prescribing useless subjects. It’s no easy task—indeed it’s very difficult—to realize that in every soul there is an instrument that is purified and rekindled by such subjects when it is blinded and destroyed by other ways of life, an instrument that it more important to preserve than ten thousand eyes, since only with it can the truth be seen (ibid.).

In distinct yet intimately related ways, the quadrivial arts serve this very purpose: to purify and rekindle the mind’s eye so that it may see the truth. In doing so, the quadrivial arts lead us through the foothills of philosophy; they help us begin the journey, pointing us in the right direction, perfecting our intellectual vision so that it is well-suited for the philosophical way of life. Through a renovation of the imagination, these arts can assist in freeing us from an undue preoccupation with and attachment to lower things. Through them the philosophical soul begins its ascent to the things themselves and what truly is.